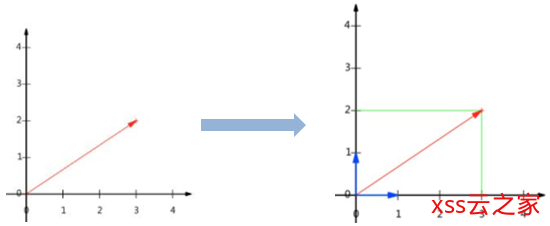
NumPy切片和索引




创建与输入数组相等长度的新数组,作为直接寻址表。两数之和的期望是Target,将Target依次减输入数组的元素,得到的值和直接寻址表比较,如果寻址表存在这个值则返回;如果不存在这个值则将输入数组中的元素插入寻址表,再进行输入数组中的下一个元素。
再进一步优化可以将输入数组直接作为直接寻址表,控制对应的下标就好,代码如下:
Code:直接寻址表
class Solution {
public int[] twoSum(int[] nums, int target) {
for (int i = 1; i < nums.length; i++) {
int temp = target - nums[i];
for (int j = 0; j < i; j++) {
if (temp == nums[j]) return new int[]{j, i};
}
}
return null;
}
}动画:直接寻址表

数组里面每一个槽位放的是8个字节,用于一个指向外部类的引用。这个外部类可以是链表对象,也可以是红黑树对象,都可以存一个或者一个以上的元素,也可以是空链表或空树。散列表在某种意义上需要的数组空间可以比直接寻址表要少的很多。

散列函数是将所有元素的键转换为自然数,自然数的数集是{0,1,2,……}。
如果所有元素的键是正整数,最常用的方法是求模(除留余数法)。我们选择长度为素数M的数组,对于任意正整数k,计算k mod M求得余数;
如果所有元素的键是浮点数,我们将它表示为二进制数,忽略小数点再转化为十进制,然后求模;
如果所有元素的键是字符串,可以将它字符串里面的每一个字符通过ASCII码转换,并相加得到这个字符串的hash,然后求模;
如果所有元素的键是对象或者组合键(对象里面的是属性类型不定),也可以通过上面的方法混合起来。

除了线性探测法,还有二次探测还有双重探测。
线性探测法是,通过散列函数得到散列值,检查这个散列值是否被占用,如果被占用,将索引增大,到达数组结尾时折回数组的开头,直到找到没有被占用的散列值。
线性探测采用的散列函数为:
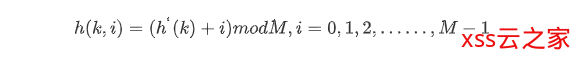
其中h`(k)是第一次通过散列函数得到的散列值。
二次探测采用的散列函数为:
编写自己的 GitHub Action,体验自动化部署
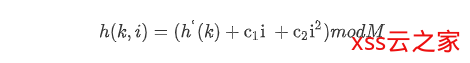
双重探测采用的散列函数为:
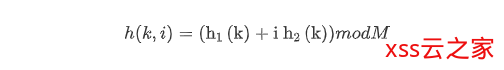
其中
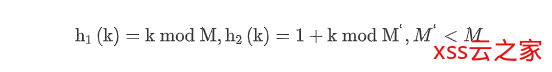

键簇,是指元素在插入数组后聚集成的一组连续的条目,决定线性探测的平均成本。
如下图所示,插入之前已经看到了两个比较长的键簇,如果待插入元素通过散列函数得到的散列值正好是这两个键簇中的第一个位置,就需要探测很多次才能找到空的位置;如果落在了两个键簇间的只有一个空位置,那就产生了更长的键簇,对线性探测的平均成本大大增加。
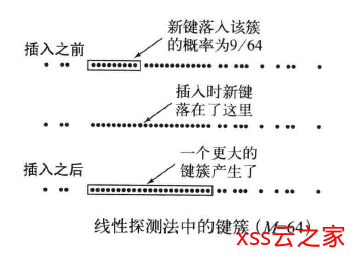
显然,短小的键簇才能保证较高的效率,不管是插入、查找还是删除算法。随着插入的键越来越多,较长的键簇越来越多,有可能插入一个元素就将两个很长的键簇合并。所以才有了两次探测和双重探测,可以降低这种情况出现。

动态空间处理其实就是改变数组的长度,可以设定一个构造函数,这个构造函数可以接受一个固定的容量作为参数。
M是目前散列表数组的长度,N是目前在散列表已插入元素的个数。如何扩容和缩容可以设定一个条件,如果N/M >= 上边界,即平均每个槽承载元素超过一定程度,就进行扩容;如果N/M <= 下边界,即平均每个槽承载元素降到一定程度,就进行缩容。
扩容和缩容都会创建一个新的长度M的散列表,散列函数也会因为M而改变,原来的所有元素通过新的散列函数重新散列并插入新的散列表中。
动画:动态空间处理
Java 8之前,每一个槽对应一个链表;
Java 8开始之后,当哈希冲突达到一定程度时,每一个位置槽从链表转成红黑树。

面试官很客气,一直送我到门口,我依依不舍地离开这个地方。嗯,面试官真是个好人。
我出去大门,看见一个面试者在拿着A4纸一直默读,我想那个面试官待会要面这个人吧。小伙子,你运气真好,希望你面试成功。

场景虚构,如有雷同,实属巧合
—–完结—–
喜欢本文的朋友,欢迎关注公众号「算法无遗策」,和我们一起学数据结构、刷算法题。
深入拆解类加载器,这样的姿势你还不懂吗?








![[AI开发]小型数据集解决实际工程问题——交通拥堵、交通事故实时告警-xss云之家](https://png.xssyun.com/xssyun/2020/1/FnY3ee.gif?x-oss-process=style/anjian)