全网最全RabbitMQ总结,别再说你不会RabbitMQ
前言
上期文章:「05」回归的诱惑:一文读懂线性回归 中 , 我们介绍了线性回归的原理,组成和优缺点,并探讨了回归的本质含义。在这一期,我们将从回归开始,引出一个机器学习中最重要的任务——分类。
还记得我们上一节的课后题吗?其实答案很简单,任意一条线都可以把任意的数据点分为不同的类,也就是有无数个直线方程存在,这种解并没有意义。这就引出了我们的主题——分类。对于分类问题来说,不同的数据必须分为不同的类别,这个类别,在机器学习中也叫作标签(label)。只有知道了类别,才可以真正进行分类学习,这叫做监督学习。
因此,线性回归的使用场景是回归,而我们这一期的主题——逻辑回归则是用于分类。关于分类和回归,该如何理解它们的区别和联系呢?往下看。

什么是回归?
分类和回归是两个相关联的概念,我们在上一篇文章讲过,以前的一位生物学家高尔顿在研究父母和孩子身高的遗传关系时,发现了一个直线方程,通过这个方程,他几乎准确地拟合了被调查父母的平均身高 x 和 子女平均身高 y 之前的关系:
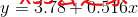
这个方程是什么意思呢?它代表父母身高每增加1个单位, 其成年子女的平均身高只增加0.516个单位,反映了一种“衰退”效应(“回归”到正常人平均身高)。虽然之后的x与 y变量之间并不总是具有“衰退”(回归)关系,但是为了纪念高尔顿这位伟大的统计学家,“回归”这一名称就保留了下来。
我们可以把回归理解为关系的找寻:回归分析是通过规定因变量和自变量来确定变量之间的因果关系,建立回归模型,并根据实测数据来求解模型的各个参数,然后评价回归模型是否能够很好的拟合实测数据,如果能够很好的拟合,则可以根据自变量作进一步预测,比如我们提到的广告费用与产品销售额的关系。
什么是分类?
所谓分类,简单来说,就是根据文本的特征或属性,划分到已有的类别中。从功能上看,分类问题就是预测数据所属的类别,比如垃圾邮件检测、客户流失预测、情感分析、犬种检测等。分类算法的基本功能是做预测。我们已知某个实体的具体特征,然后想判断这个实体具体属于哪一类,或者根据一些已知条件来估计感兴趣的参数。比如:我们已知某个人存款金额是10000元,这个人没有结婚,并且有一辆车,没有固定住房,然后我们估计判断这个人是否会涉嫌信用欺诈问题。这就是最典型的分类问题,预测的结果为离散值,当预测结果为连续值时,分类算法就退化为之前所说的的回归模型。
二分类
我们先来看看什么是二分类:
给定不同种类数据点,二分类就是找到一条线,使得不同的数据点位于这条线的两侧。一般来说,只存在一条唯一的直线方程,也就是y = f(x),让分类点之间的误差距离最小,比较直观的解法就是SVM,以后会谈到。这里我们用下面这张图举个例子:
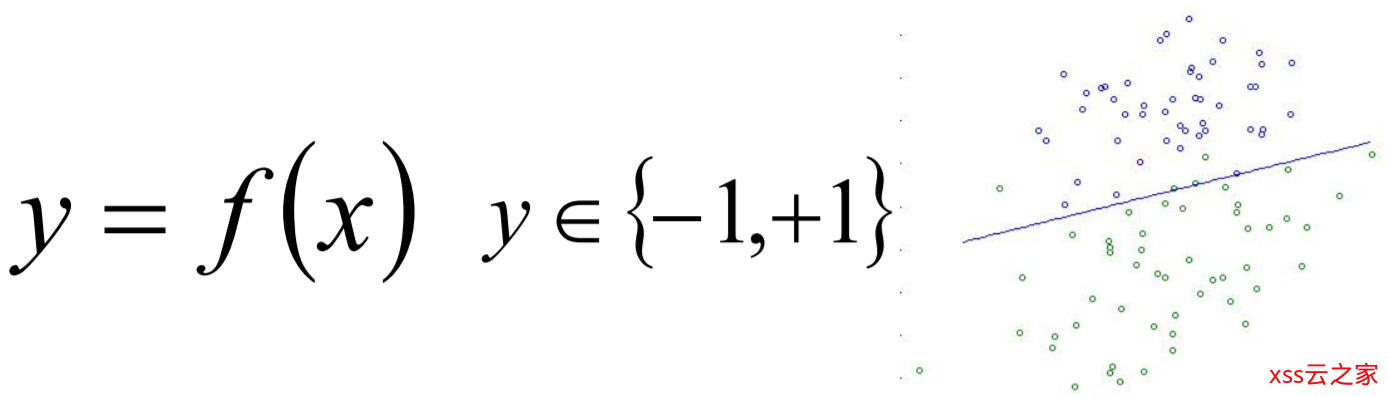
可以看到,图中的2类数据分别是蓝点和绿点。已经知道了这条直线方程,那如何把新出现的数据点根据数据类别的不同划分成不同的类?只需要判断它是在直线的上面(紫色点)还是下面(绿色点)就行了。
多分类
那么,如果存在两种以上的数据且混合分布在一起,要怎么划分呢?一条直线显然已经无法划分了,需要多个直线/平面,甚至是曲线进行划分,这个时候的参数方程就不是直线方程了,而是更复杂的多次项方程。不过我们也可以用很多条直线来近似的拟合这种曲线。这里也涉及到机器学习的灵魂拷问:过拟合,在后面的一期文章,我们会单独聊聊它,这里先按下不表。
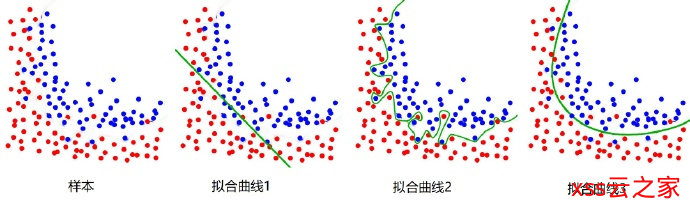
所以,多分类问题其实可以看成二分类的扩展版,同样待预测的label标签只有一个,但是label标签的取值可能有多种情况;直白来讲就是每个实例的可能类别有K种(t1 ,t2 ,…tk ,k≥3):
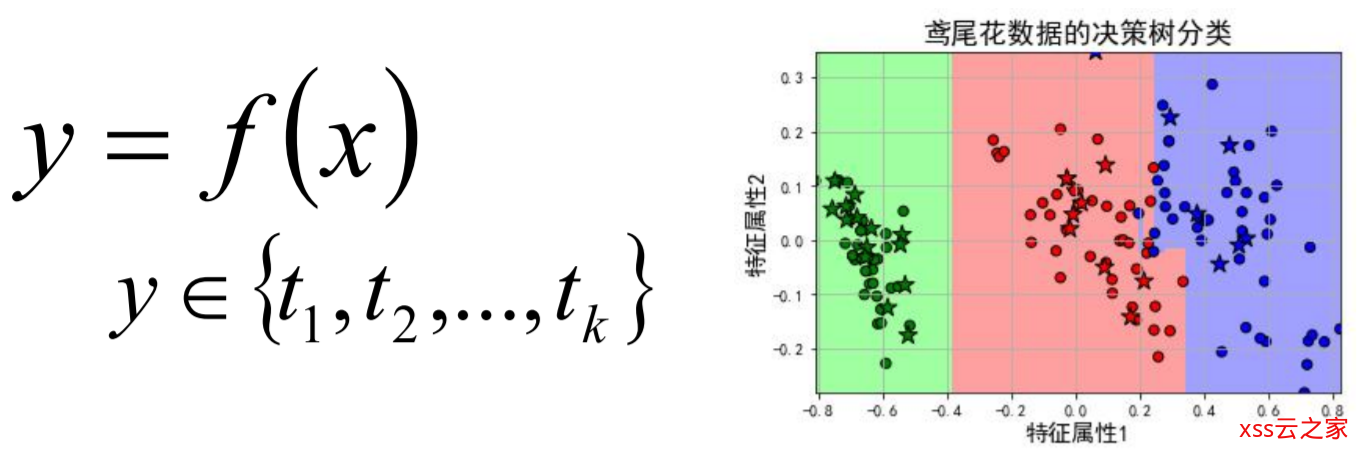
上面的解释只是一个直观上的理解,现在给出严格的定义:分类,是在一群已经知道类别标签的样本中,训练一种分类器,让其能够对某种未知的样本进行分类。
分类算法属于一种有监督的学习,而分类过程就是建立一种分类模型来描述预定的数据集,通过分析由属性描述的数据库元组来构造模型。分类的目的就是使用分类对新的数据集进行划分,其主要涉及分类规则的准确性、过拟合、矛盾划分的取舍等。分类算法分类效果如图所示。
分类的应用场景
- 判断邮件是否为垃圾邮件
- 判断在线交易是否存在潜在风险
- 判断肿瘤为良性还是恶性等等
回归与分类
分类和回归是如今机器学习中两个不同的任务,而属于分类算法的逻辑回归,其命名有一定的历史原因。这个方法最早由统计学家David Cox在他1958年的论文《二元序列中的回归分析》(The regression analysis of binary sequences)中提出,当时人们对于回归与分类的定义与今天有一定区别,只是将“回归”这一名字沿用了。实际上,将逻辑回归的公式进行整理,我们可以得到
所以,回归算法,有时候是相对分类算法而言的,与我们想要预测的目标变量y的值类型有关。如果目标变量y是分类型变量,如预测用户的性别(男、女),预测月季花的颜色(红、白、黄……),预测是否患有肺癌(是、否),那我们就需要用分类算法去拟合训练数据并做出预测;如果y是连续型变量,如预测用户的收入(4千,2万,10万……),预测员工的通勤距离(500m,1km,2万里……),预测患肺癌的概率(1%,50%,99%……),我们则需要用回归模型。
聪明的你一定会发现,有时分类问题也可以转化为回归问题,例如刚刚举例的肺癌预测,我们可以用回归模型先预测出患肺癌的概率,然后再给定一个阈值,例如50%,概率值在50%以下的人划为没有肺癌,50%以上则认为患有肺癌。
我们可以这么理解:
分类问题预测数据所属的类别:比如垃圾邮件检测、客户流失预测、情感分析、犬种检测等。
回归问题根据先前观察到的数据预测数值,比如销量预测,房价预测、股价预测、身高体重预测等。
分类算法中,待分析的数据是一个一个处理的,分类的过程,就像给数据贴标签的过程,来一个数据,我放到模型里,然后贴个标签。聚类算法中,待分析的数据同时处理,来一堆数据过来,同时给分成几小堆。因此,数据分类算法和回归算法的最大区别是时效性问题。在已有数据模型的条件下,数据分类的效率往往比数据聚类的效率要高很多,因为对于分类来说,一次只是一个对象被处理,而对于回归结果来说,每当加入一个新的分析对象,整个直线方程都有可能发生改变,因此很有必要重新对所有的待分析对象进行计算处理。
什么是逻辑回归?
Logistic 回归是机器学习从统计学领域借鉴过来的另一种技术。它是二分类问题的首选方法。像线性回归一样,Logistic 回归的目的也是找到每个输入变量的权重系数值。但不同的是,Logistic 回归的输出预测结果是通过一个叫作「logistic 函数」的非线性函数变换而来的。
逻辑回归(Logistic Regression)就是一种分类分析,它有正向类和负向类,即:y ∈ {0, 1},其中 0 代表负向类,1 代表正向类。当面对一个分类问题:y = 0 或 1,可能出现的情况是: y > 1 或 < 0,就无法进行结果的归纳。逻辑(logistic) 函数的形状看起来像一个大的「S」,所以也叫S回归。
我们知道,线性回归模型产生的预测值

是一个任意实值,于是,我们需将实值z 转换为0到1之间的值. 最理想的是“单位阶跃函数” (unit-step function)。假设我们有一个Z作为已经计算出来的实值,比如5,那么在经过S函数的映射后,它就是变成一个[0, 1]区间的小数,比如0.75,根据这个数我们可以判断最终预测值y的类别
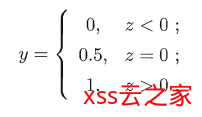
也就是将分类的阈值假设为0.5,如果Z大于0.5,就是正类,反之则是负类。这里0.75 > 5,所以输出1。当然,阈值并非固定,可以设置为任一合理的数值。

但是,从上面的图可以看到,单位阶跃函数不连续,因此直接使用的效果并不好。我们能否找到能在一定程度上近似单位阶跃函数的”替代函数” (surrogate function) ,并希望它单调可微呢?
答案是可以,这就是逻辑函数(logistic function) 。逻辑函数的公式如下:

它会把任何值转换至 0-1 的区间内,这十分有用,因为和阶跃函数一样,我们可以把任何一个阈值应用于logistic 函数的输出,从而得到 0-1 区间内的小数值(例如,将阈值设置为 0.5,则如果函数值小于 0.5,则输出值为 1),并预测类别的值。得到的结果可以满足:0 <= y <= 1,也可以说逻辑回归是一种特殊的分类算法。
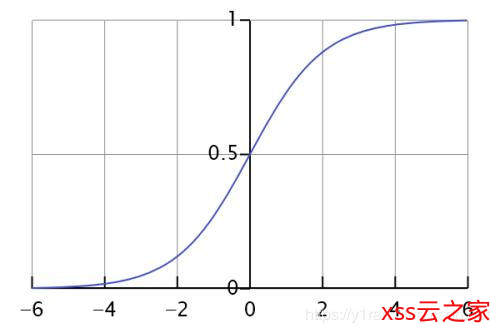
逻辑回归是当前业界比较常用的机器学习方法,它与多元线性回归同属一个家族,即广义线性模型。由于模型的学习方式,Logistic 回归的预测结果也可以用作给定数据实例属于类 0 或类 1 的概率,这对于需要为预测结果提供更多理论依据的问题非常有用。与线性回归类似,当删除与输出变量无关以及彼此之间非常相似(相关)的属性后,Logistic 回归的效果更好。该模型学习速度快,对二分类问题十分有效。
逻辑回归的本质
所有的分类问题都是一个优化问题,本质上是一个极小化问题,只是模型的代价函数构造不同,本质上分类问题可以理解为一种离散的回归。
1. 逻辑回归与线性回归的关系
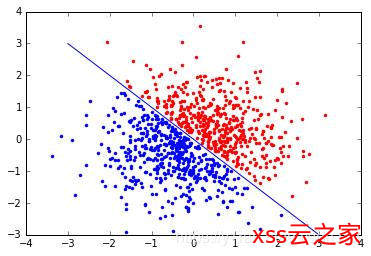
简单来说,多元线性回归是直接将特征值和其对应的概率进行相乘得到一个结果,逻辑回归则是在这样的结果上加上一个逻辑函数。以下图为例,不同的类别(X和O)分布在水平的位置。如果直接使用线性回归做拟合,学习到的直线只能保证各个点到线上的误差最小,却无法使两种数据分到不同的一侧。
xLua下使用lua-protobuf

逻辑回归处理的是分类问题,线性回归处理的是回归问题,这是两者的最本质的区别。逻辑回归中,因变量取值是一个二元分布,模型学习得出的是
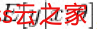
即给定自变量和超参数后,得到因变量的期望,并基于此期望来处理预测分类问题。而线性回归中实际上求解的是

是对我们假设的真实关系

的一个近似,其中代表误差项,我们使用这个近似项来处理回归问题。在关于逻辑回归的讨论中,我们均认为y是因变量,而非,这便引出逻辑回归与线性回归最大的区别,即逻辑回归中的因变量为离散的,而线性回归中的因变量是连续的。
换句话说,逻辑回归模型就是在拟合

这条直线,使得这条直线尽可能地将原始数据中的两个类别正确的划分开,而这就是我们所说的广义线性模型之一。
广义线性模型
我们说过,线性回归是直接将特征值和其对应的概率进行相乘得到一个结果,逻辑回归则是在这样的结果上加上一个逻辑函数。在自变量x与超参数θ确定的情况下,逻辑回归可以看作广义线性模型(Generalized Linear Models)在因变量y服从二元分布时的一个特殊情况,而使用最小二乘法求解线性回归时,我们认为因变量y服从正态分布。
当然,逻辑回归和线性回归也不乏相同之处,首先我们可以认为二者都使用了极大似然估计来对训练样本进行建模。线性回归使用最小二乘法,实际上就是在自变量x与超参数θ确定,因变量y服从正态分布的假设下,使用极大似然估计的一个化简;而逻辑回归中通过对似然函数
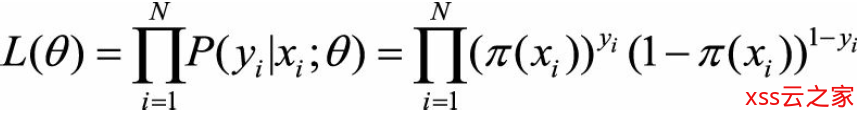
的学习,得到最佳参数θ。另外,二者在求解超参数的过程中,都可以使用梯度下降的方法,这也是监督学习中一个常见的相似之处。
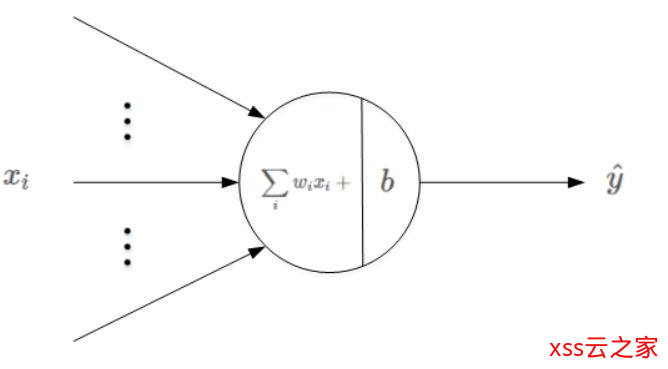
有接触过深度学习基础的同学知道,深度神经网络是由N层具有激活函数的隐藏单元组成的,在这里我们可以把逻辑回归看做一个1层的浅层神经网络(这个引申自Lecun的调侃说法,严谨的同学请忽略~),激活函数就是Sigmoid函数,中间是线性映射,只学习一个隐藏层的参数。
为什么叫逻辑回归?
logistic regression,在英语的术语里准确而简洁,但是翻译成中文则有多种译法,例如:逻辑回归(比较常见),对数几率回归(周志华),逻辑斯谛回归(Understanding Machine Learning:From Theory to Algorithms中译本)。之所以成为逻辑回归,是因为Logit这个词。
对数几率函数,又叫做”Sigmoid 函数”,它将z 值转化为一个接近0 或1 的υ 值并且其输出值在z 一0 附近变化很陡。把我们前面提到过的分类、线性回归以及逻辑函数结合起来,就能得到如下公式:

这就是逻辑回归的最终形态,也就是我们这篇文章的核心——逻辑回归公式。
现在,让我们用高中数学做一个简单的变形,将公式两边同时取对数
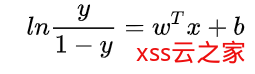
因为在定义上,我们将 y 视为 x 为正例的概率,则1-y 就是数据点x为反例的概率(基本的概率论知识)。两者的比值称为几率(odds),统计上指该事件发生与不发生的概率比值,若事件发生的概率为 p。则对数几率:

将y视为类后验概率估计,重写公式有:
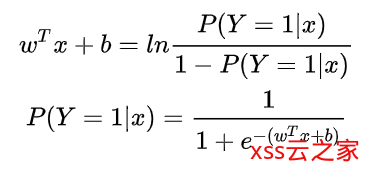
也就是说,输出 Y=1 的对数几率是由输入 x 的线性函数表示的模型,这就是逻辑回归模型。当 
的值越接近正无穷,

概率值也就越接近 1。因此逻辑回归的思路是,先拟合决策边界(不局限于线性,还可以是多项式),再建立这个边界与分类的概率联系,从而得到二分类情况下的概率。
如果把一个事件的几率(odds)定义为该事件发生的概率与该事件不发生的概率的比值
那么逻辑回归可以看作是对于“y=1|x”这一事件的对数几率,借助逻辑函数进行的线性回归,于是“逻辑回归”这一称谓也就延续了下来。
为什么要用对数几率?
对于二分类问题, 
样本 Xi 属于正例1的概率定义为 P1 ,属于负例0的概率定义为 P2,由于事件独立,我们知道P1 + P2 = 1。
比如,样本Xi属于正例,则应有
,即:
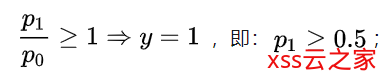
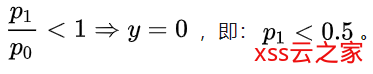
显然,只需对
与1的关系进行建模,即可区分样本的类别。
我们思考一下,使用对数几率的意义在哪?通过上述推导我们可以看到 Logistic 回归实际上是使用线性回归模型的预测值逼近分类任务真实标记的对数几率,其优点有:
- 直接对分类的概率建模,无需实现假设数据分布,从而避免了假设分布不准确带来的问题;
- 不仅可预测出类别,还能得到该预测的概率,这对一些利用概率辅助决策的任务很有用;
- 对数几率函数是任意阶可导的凸函数,有许多数值优化算法都可以求出最优解。
逻辑回归的局限
1)对模型中自变量多重共线性较为敏感,例如两个高度相关自变量同时放入模型,可能导致较弱的一个自变量回归符号不符合预期,符号被扭转。需要利用因子分析或者变量聚类分析等手段来选择代表性的自变量,以减少候选变量之间的相关性;
2)预测结果呈“S”型,因此从log(odds)向概率转化的过程是非线性的,在两端随着log(odds)值的变化,概率变化很小,边际值太小,slope太小,而中间概率的变化很大,很敏感。 导致很多区间的变量变化对目标概率的影响没有区分度,无法确定阈值。
例子说明
假如支付宝的算法团队想要构建一个模型来决定是否通过用户的花呗提额申请,它将预测客户的还款是否会“违约”。
 首先对变量之间的关系进行线性回归以构建模型,我们将分类的阈值假设为0.5。
首先对变量之间的关系进行线性回归以构建模型,我们将分类的阈值假设为0.5。
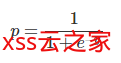
然后将Logistic函数应用于回归分析,得到两类的概率。该函数给出了事件发生和不发生概率的对数。最后,根据这两类中较高的概率对变量进行分类。这里,逻辑回归学习出来的也是一条直线,如果新的用户通过计算,位于直线的右上,则有潜在违约风险,需要拒绝申请。反之则是安全的。此外,越远离直线,则分类正确的置信度也越高。
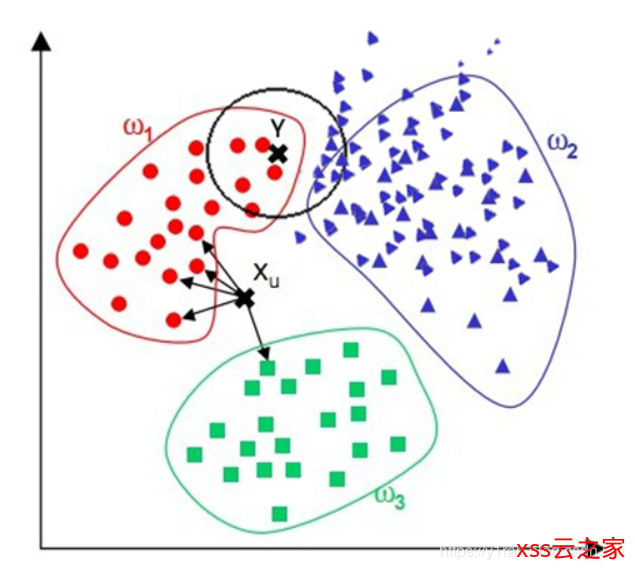
课后习题
对于已知的三类数据,红色点、蓝色三角和绿色方块,是否可以用逻辑回归对其进行分类?如果可以,要怎样使用?如果不行,又是因为什么?
结语
最后,下一篇文章将会从逻辑回归的参数学习方式谈起,讲讲极大似然估计和牛顿法~在这之前,可以先将实战代码自己实践一下:「08」回归的诱惑:深入浅出逻辑回归(Python实战篇)
参考文献
- 《机器学习》周志华
- 《动手学深度学习》MXNet Community
- An Introduction toStatistical Learning with Applications in R
- 知乎:来!一起捋一捋机器学习分类算法
- 知乎:机器学习:分类算法(Classification)
- 百面机器学习,葫芦娃
Qt Installer Framework翻译(5-1)








![[AI开发]小型数据集解决实际工程问题——交通拥堵、交通事故实时告警-xss云之家](https://png.xssyun.com/xssyun/2020/1/FnY3ee.gif?x-oss-process=style/anjian)